Creating new animation types

It’s a fairly uncommon scenario to want to animate a type that’s not already built into WPF. But when you do, it takes quite a lot of work, mostly hacking it with Reflector to explore this undocumented venue.

One day I needed to animate the CornerRadius of a Border. Don’t ask me why, it just happened. I was a bit surprised to find out that almost all animations have the (almost) exact same implementation, but no code was shared. Meaning, if you had to create a new one, all the code would have to be copied.

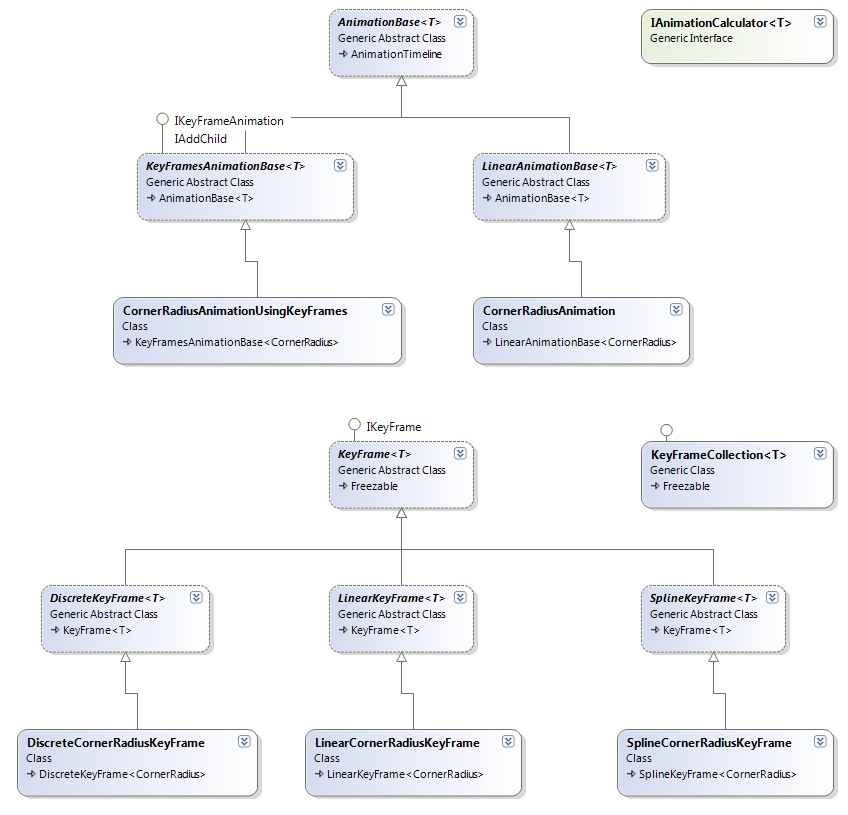
All animations inherit from AnimationTimeline. Each one has a base class TAnimationBase, and a few possible implementations: TAnimation (a linear animation), TAnimationUsingKeyFrames and (the more rare) TAnimationUsingPath. Note the T. Does it remind you of something? If you said “generics”, you were right. I may be overlooking something, since WPF is such a vast framework, whose designers must have had a much broader view to make such decisions, but I think this could have been implemented a bit better. Here’s how.

When I wrote a paper about CLR generics for my university, I stumbled upon a problem some of you may have also encountered: How can I use arithmetic operators on a generic type? In C++ it’s rather easy: the compiler checks the template by call when it performs the macro-expansion. So if you write:

template<class T> class MyClass
{
    T MyMethod(T a, T b) { return a + b; }
}

That would compile just fine. It would only throw compilation errors when you try to instantiate MyClass<T> where T doesn’t support the “+” operator. In C#, you simply can’t do that (unless you use casting and a lot of ifs – an ugly solution), since you can only constrain using interfaces and base classes. Because numeric types have no such common ancestor, you’re in a pickle.

Anders Hejlsberg has lectured about a possible solution for this issue: create a calculator class. I shall demonstrate using the calculator interface I created for the animation:

public interface IAnimationCalculator<T>
    where T : struct
{
    T Add(T value1, T value2);
    T Subtract(T value1, T value2);
    T Scale(T value, double factor);
    T Interpolate(T from, T to, double progress);
    T GetZeroValue(T baseValue);
    double GetSegmentLength(T from, T to);
    bool IsValidAnimationValue(T value);
}

I constrained T to be a value type. I assumed most of the types we’d like to animate are lightweight structures, but this restriction can be removed. And so, I created the other classes, according to the scheme I mentioned above:

Implementers have very few things to do: create an IAnimationCalculator for their type, inherit from the desired classes, override the abstract methods (very few and usually freezable-related, and of course the CreateCalculator() method) and add constructors (just call the ones from the base.) In the attached project you’ll find a sample implementation for the CornerRadius type.

One last caveat: I did not test this on a type other than CornerRadius. It’s quite possible this small framework will not fit every scenario. As I said, the designers of WPF may very well have had a good reason not to take this approach.

Update: I’ve changed the implementation from a calculator type parameter to a CreateCalculator() abstract method. This makes my classes slightly more cumbersome, but more importantly, makes writing polymorphic code a lot nicer (consider writing a method that accepts a LinearAnimationBase. Why should you have to drag along that TCalc type parameter?)